지난 장에서 단어를 표현하기 위한 방법으로 두 가지를 알아보았다.
첫째는 사전처럼 Signifier - Signified 구조로 나타나지는 Denotational Semantics(표시론적 의미론)
두 번째는 단어의 분포특성을 파악하여 유사성을 통한 방법인 Distributional Semantics(분산적 의미론, 분포 의미론)
이번 장에서는 Distributional Semantics을 나타낼 수 있는 프레임 워크 중 가장 기본적인 Word2Vec을 살펴보자.
Word Vector
단어의 유사성을 표현하기 위해서 어떻게 표현할 수 있을까.
문맥에서 발생하는 단어를 벡터로 보는 것이다.
$$ banking = \begin{bmatrix} 0.286 \\ 0.792 \\ -0.177 \\ -0.107 \\ 0.109 \\ -0.542 \\0.349 \\ 0.271 \\ \end{bmatrix} $$
해당되는 단어만 1로 표시하고 나머지는 0으로 표시한 One-Hot Encoding과 다르게, 단어에 대해서 Desne Vector를 구축하여 해당 단어의 의미를 나타낼 것이다. 이런 식으로 벡터를 나타내면 벡터가 문맥에서 다른 단어가 나타나는 데에 유용하다고 한다.
Why? : One-Hot Encoding의 희소 표현이 (해당 단어만 1이고 나머진 0이니까) 고차원의 각 차원이 분리된 표현 방법이었다면, 분산 표현은 단어의 의미를 보다 낮은 저차원에 여러 차원에다가 분산하여 표현하는 것이다. 이런 표현 방법을 사용 시 단어 벡터 간의 유의미한 유사도를 계산할 수 있다.
*위의 수식에는 8차원 정도로 나타냈지만 실제로는 더 크게 사용한다. (300 차원 정도)
Word vector 는 Word Embedding, (Neural) Word Representation, Distributed Representation 으로 부르기도 한다.
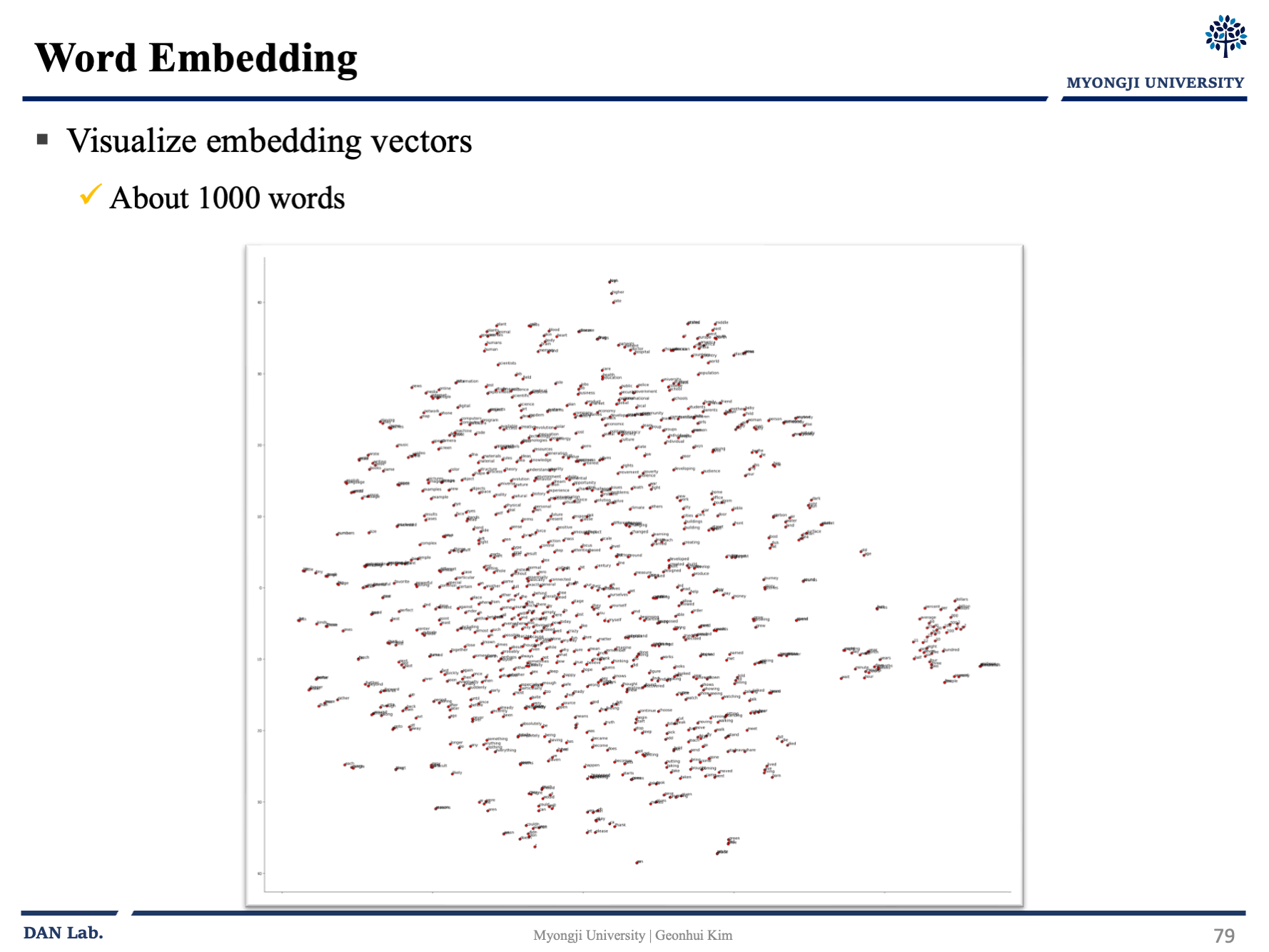
Word Vector로 단어를 임베딩 하고 난 후 결과를 한번 시각화해보자
시각화한 것을 보고 나면 꽤나 그럴 듯 하나고 느낄 것이다.

사진을 보면 playing, games, play 가 근접하게 있고, wrote writing, books 등 우리가 생각하기에 비슷하다고 느낀 단어들이 가까이 있음을 알 수 있다.
해당 예제는 몇십만 개의 단어를 100차원의 dense vector로 줄인 것으로 사람이 보기에는 100차원도 크기 때문에, 유사도를 판단하기 힘들어 우선 2차원으로 시각화를 하였다.
100차원에서 2차원으로 줄이면서 정보의 손실이 일어났을 수도 있다.
Word2Vec: Overview
https://arxiv.org/abs/1301.3781
Efficient Estimation of Word Representations in Vector Space
We propose two novel model architectures for computing continuous vector representations of words from very large data sets. The quality of these representations is measured in a word similarity task, and the results are compared to the previously best per
arxiv.org
Word2vec 이란 단어를 벡터로 표현하기 위한 프레임워크이다.
CS224n 강의에서는 간단하며 이해하기 쉬운 시작점이라고 소개하였다 한다.
해당 프레임워크의 메인 아이디어는 아래와 같다
- 엄청나게 큰 corpus("body") of text 를 가진다
- corpus of text란 텍스트의 본문을 뜻한다. 즉 엄청나게 많은 양의 텍스트 본문을 가지고 있다고 하고 시작한다.
- 매우 희귀한 단어의 몇몇을 제거하고 고정 어휘를 모두 단어 벡터로 표현한다.
- 임의의 벡터 값으로 단어를 바꾸었으니 이제 우리는 각 단어에 대한 좋은 벡터값이 무엇인지 알아내야 한다.
- 중심 단어인 $c$와 주변(문맥) 단어 $o$의 단어 벡터의 유사성을 사용하여 $c$ 가 주어졌을 때 $o$의 확률을 계산한다 (그 반대로도 가능)
- Skip gram(중심 단어가 주어졌을 때 문맥단어를 예측)
- CBOW(주변 단어가 주어졌을 때 중심단어를 예측)
- 확률을 $maximize$ 하기 위해서 word vector를 조정한다.
대충 아래의 그림과 같이 흘러간다고 보면 좋을 것 같다.
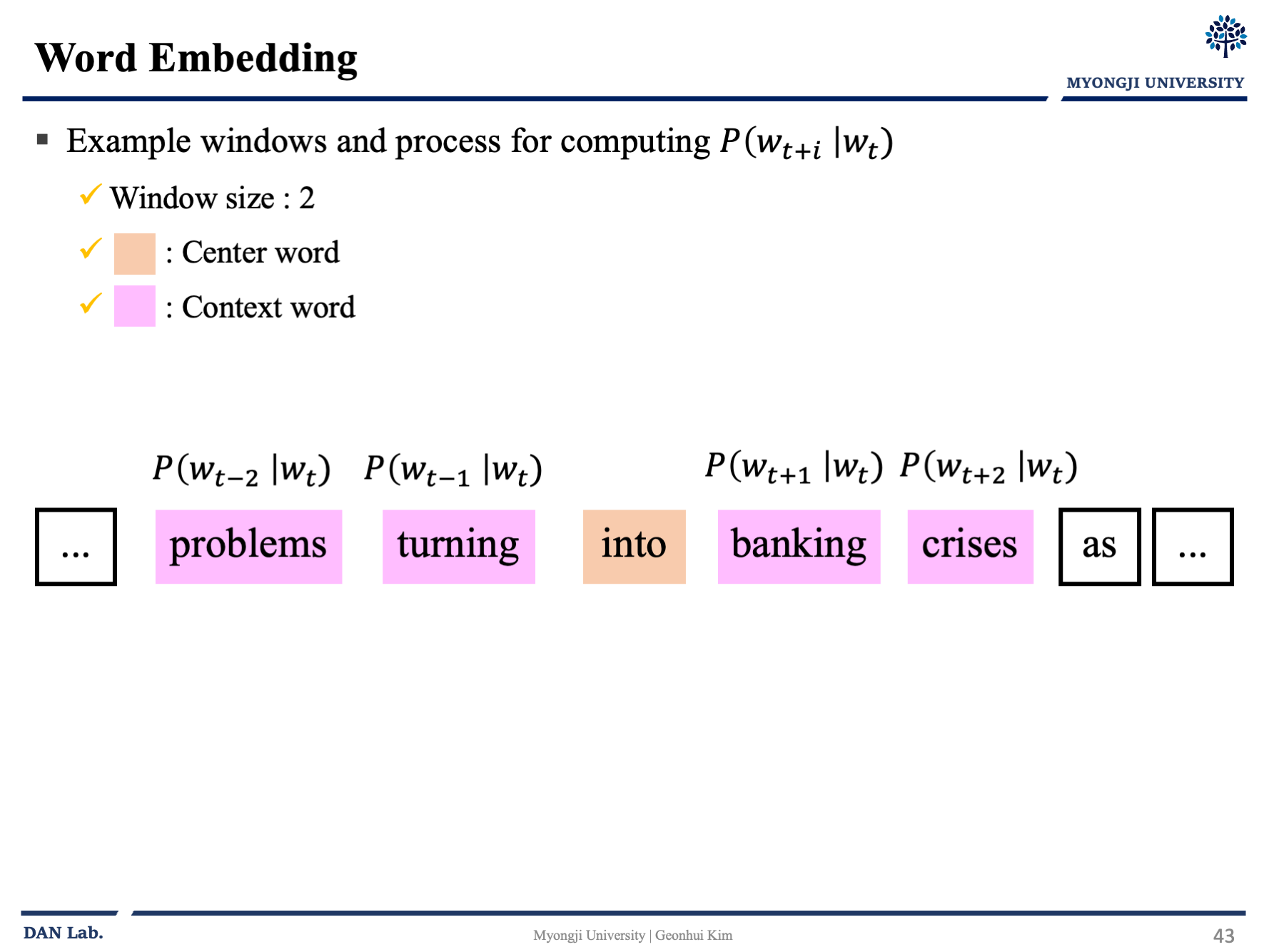
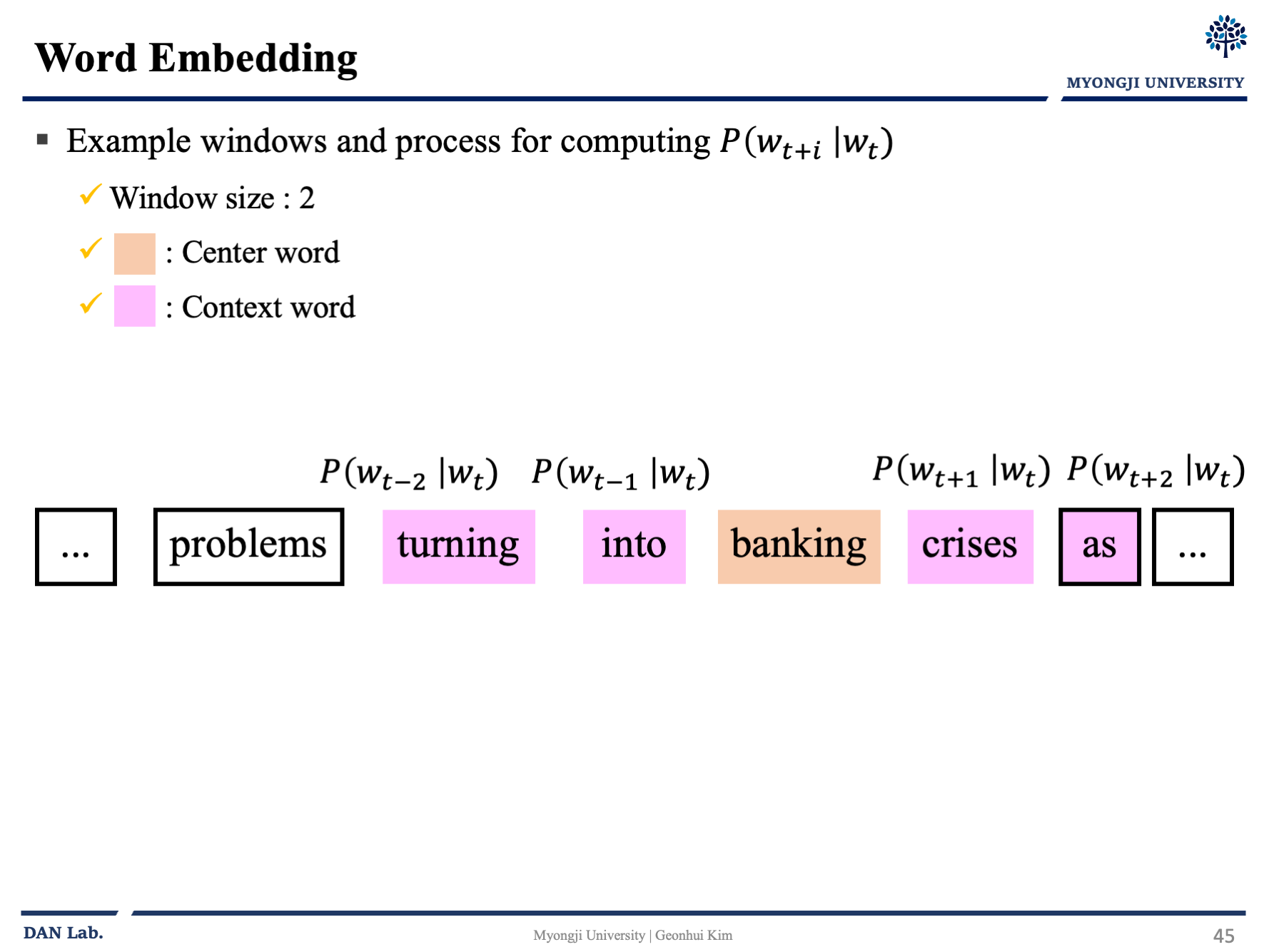
중심 단어를 선택하고 이 단어벡터를 통해 문맥 단어가 나올 확률을 예측하고 벡터를 조정하고 다음으로 넘어가고 확률을 구하고 다시 조정하고 하는 일련의 과정을 반복하는 것이다.
그럼 이런 의문점이 있을 것이다. 그러면 우리는 "중심 단어의 근처에 위치한 문맥 단어를 나올 확률을 계산하기 위해서 무엇을 해야하는가?" 이것이 word2vec의 핵심 부분이다.
Word2Vec: Objective function
Word2Vec의 목적함수는 아래와 같다.
$$Likelihood = L(\theta)=\prod_{t=1}^T \prod_{-m \le j \le m \\ \ \ \ j \ne 0} P(w_{t+j}|w_{t};\theta)$$
해당 수식을 나는 "모든 전체 텍스트에 대해서 1번째 텍스트부터 끝의 T까지 돌건데 좌우 윈도우 사이즈 m칸 내의 워드를 Center word $w_t$가 주어졌을 때의 확률을 값들이 나온다. 그리고 이 확률 값들을 최대화 하기 위해서 theta를 조정한다. " 라고 이해했다.
다시 말하면 우리의 목적은 윈도우 사이즈 안에서 문맥 단어가 발견될 확률을 최대화 하는 것이 목표이다.
$\theta$는 우리가 최적화 해야할 것이고 veter representation 이다. 조금 아래에 그림을 보면 어느 부분인지 감이 올 것 같다.
강의해서는 사람은 최대화 하는 것보다 최소화하는 것에 더욱 편하다? 뭐 이런식으로 말을하고 곱연산 보다는 합연산이 컴퓨팅에서 더 이득을 가져오기에 합연산으로 바꾸기 위해 Log를 씌운다.
결국 negative log 를 적용해서 아래의 수식으로 변화한다.
$$J(\theta)=-\frac{1}{T}\log{L}(\theta)=-\frac{1}{T}\log \sum_{t=1}^T \sum_{-m \le j \le m \\ \ \ \ j \ne 0} \log{P}(w_{t+j}|w_t;\theta)$$
* Objective function(목적함수는) cost or loss function 이라고 부르기도 한다.
위의 식변화를 통해서 목적함수를 최소화 하는 것이 예측 확률을 최대화 하는 것과 동일하게 되었다.
근데 $P(w_{t+j}|w_t)$ 확률 어떻게 구할까?
아래의 수식을 보자
$$P(o|c) = \frac{\exp(u_o^T v_c)}{\sum_{w=1}^T exp(u_w^T v_c)}$$
문맥단어 벡터 $u_o$를 중심단어 $v_c$와 내적을 통해 값을 구하고 소프트 맥스를 통해서 나머지 단어들의 값을들 가져와 확률을 구해주면 된다.
아래의 그림 예제를 통해서 한번 알아보자
Word2Vec: Example 1
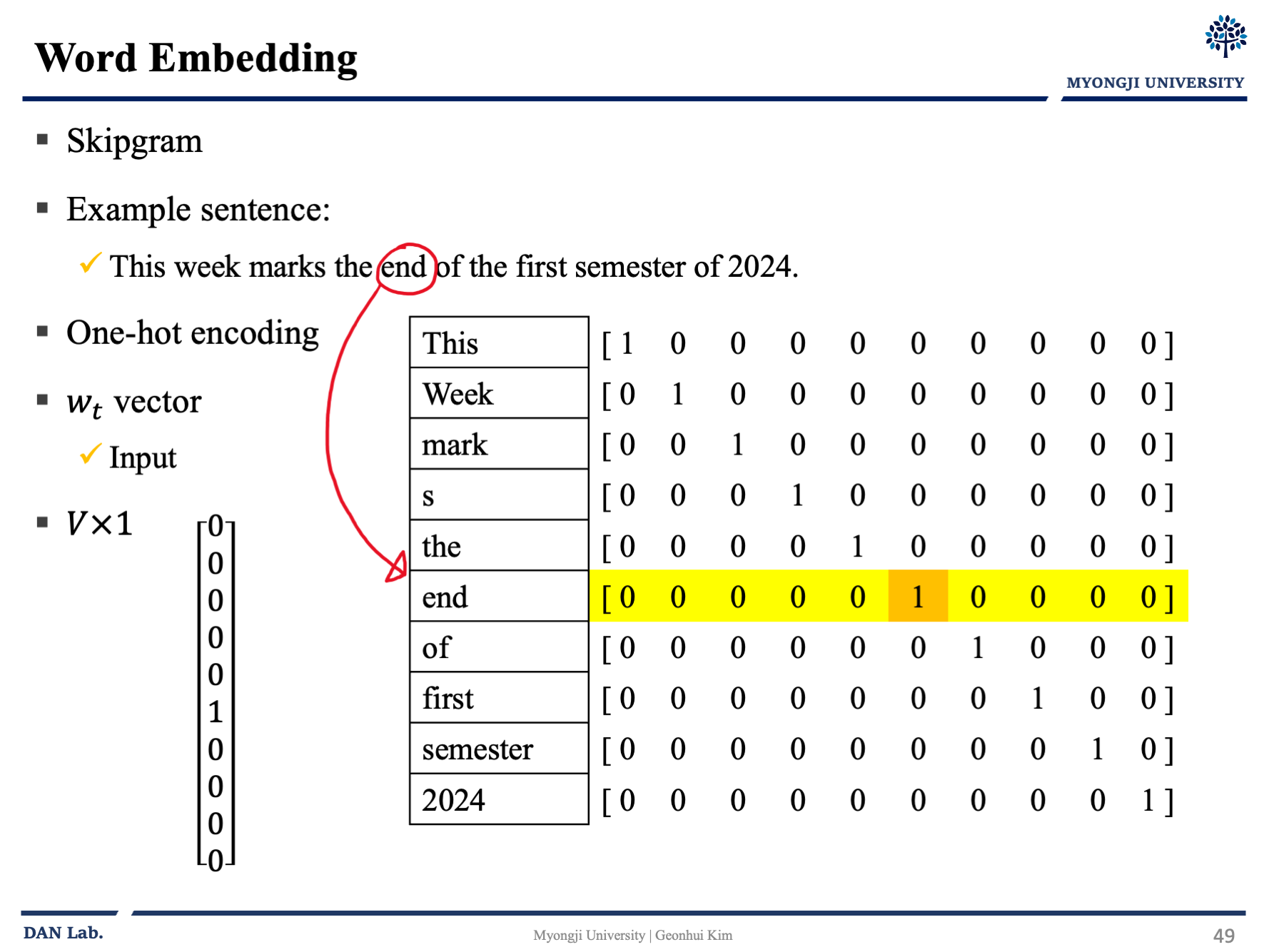
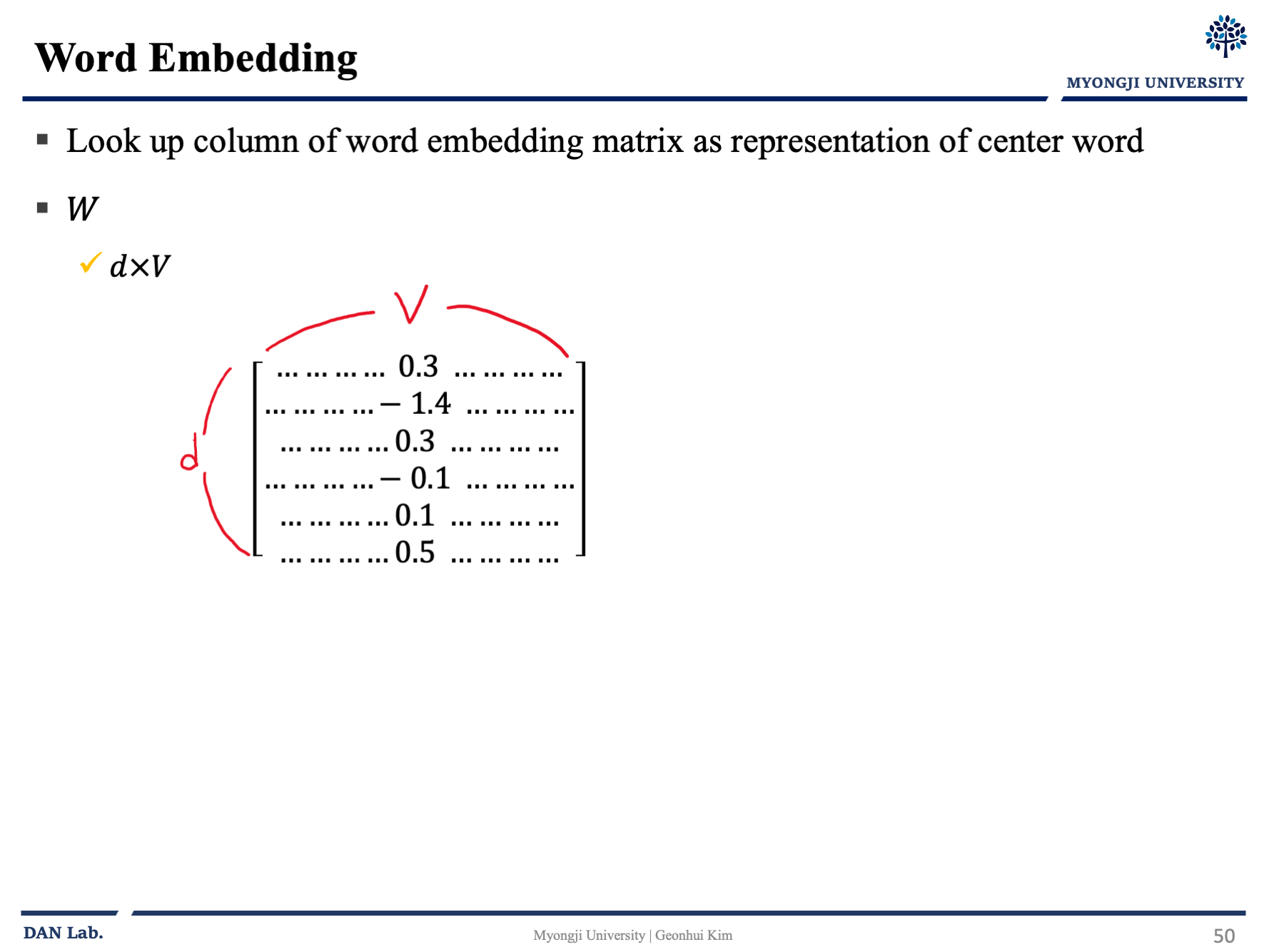





그냥 보고 넘기면 좋을 것 같다.

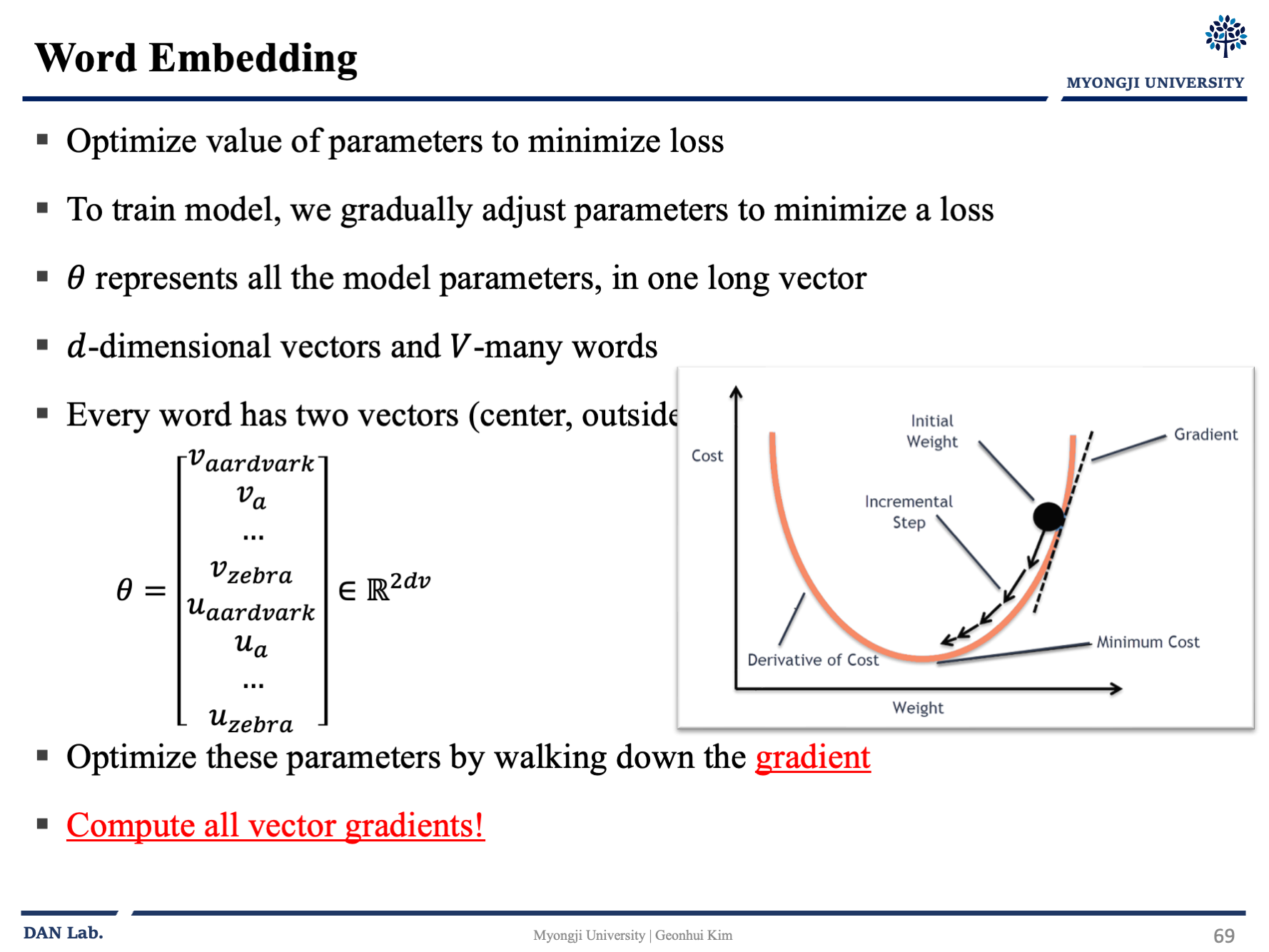
그래서 학습하면서 Loss를 줄이기 위하여 조정하는 부분은 one-hot encoding 벡터를 dense 한 representation vector로 바꿔주는 행렬 $W$와 center vector를output vector로 연결지어주는 $W'$를 조정한다.
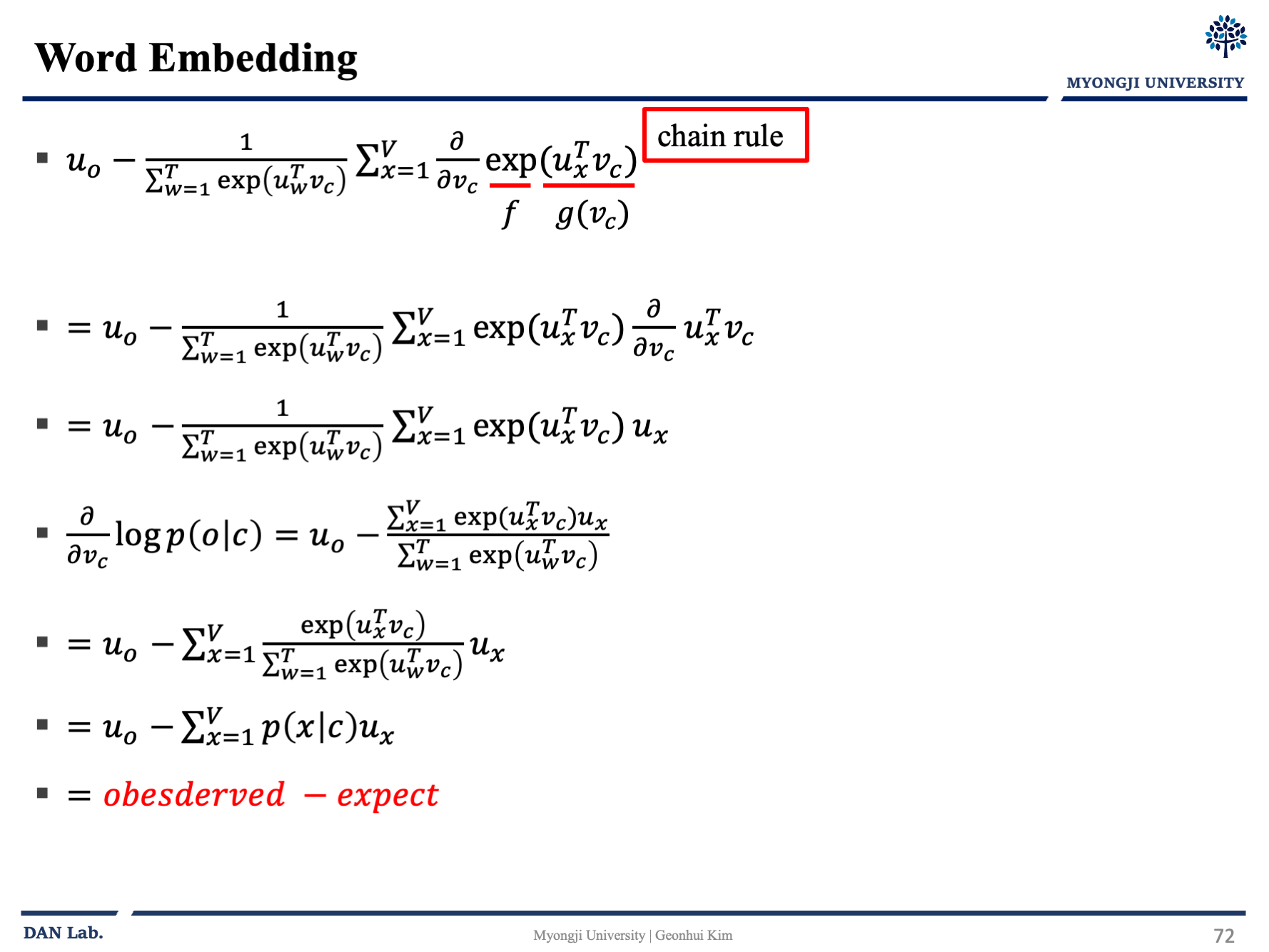
gradient 부분의 자세한 사항은 넘어가겠다. (해당 수업에서 gd, sgd, backpropagation 등을 다른 분이 발표함..)
ppt 만 보고 넘어가장
또한 Word2Vec의 최적화에 대한 추가 내용들은 여기서 다 다루면 너무 길어서 우선 넘어간다...


Word2Vec: Example 2
예제로는 Word2Vec을 이용한 예제이다. 아래의 링크를 참고했다.
09-03 영어/한국어 Word2Vec 실습
gensim 패키지에서 제공하는 이미 구현된 Word2Vec을 사용하여 영어와 한국어 데이터를 학습합니다. ## 1. 영어 Word2Vec 만들기 파이썬의 gensim 패키지…
wikidocs.net







여기까지가 Word Embedding에 대한 내용이었다. Glove 라던가 평가 방법은 나중에 다른 글로 덧붙여서 작성하는게 나을 것 같다..
'AI,ML' 카테고리의 다른 글
| NLP - [3] LSTM RNN (1) | 2024.09.23 |
|---|---|
| NLP - [2] Language Model, RNN - (3) (0) | 2024.07.21 |
| NLP - [2] Language Model, RNN - (2) (0) | 2024.06.21 |
| NLP - [2] Language Model, RNN - (1) (1) | 2024.06.17 |
| NLP - [1]Introduction (0) | 2024.03.28 |



